Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?

Как посчитать отклонение в процентах в Excel

Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.

Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.

Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2

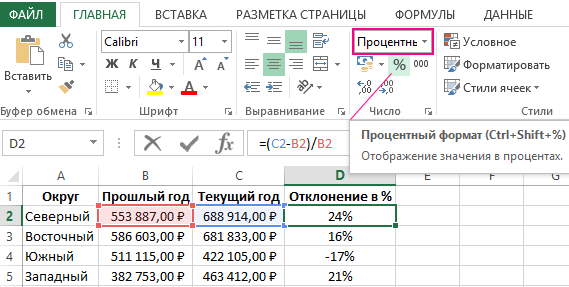
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.

Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.



Альтернативная формула для вычисления процента отклонения в Excel

В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.

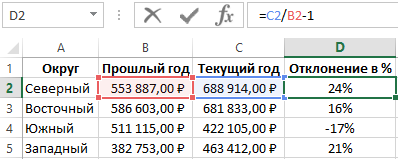
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.

Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.

Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.

Факторные эксперименты применяются тогда, когда необходимо проверить сложные гипотезы о взаимосвязях между переменными. Общий вид подобной гипотезы: «Если Аь А2, …, Ап, то В». Такие гипотезы называются комплексными, комбинированными и др. При этом между независимыми переменными могут быть различные отношения: конъюнкции, дизъюнкции, линейной независимости, аддитивные или мультипликативные и др. Факторные эксперименты являются частным случаем многомерного исследования, в ходе проведения которого пытаются установить отношения между несколькими независимыми и несколькими зависимыми переменными. В факторном эксперименте проверяются одновременно, как правило, два типа гипотез:

• 1) гипотезы о раздельном влиянии каждой из независимых переменных;
• 2) гипотезы о взаимодействии переменных, а именно — как присутствие одной из независимых переменных влияет на эффект воздействия на другой.

Факторный эксперимент строится по факторному плану. Факторное планирование эксперимента заключается в том, чтобы все уровни независимых переменных сочетались друг с другом. Число экспериментальных групп равно числу сочетаний уровней всех независимых переменных.

Сегодня факторные планы наиболее распространены в психологии, поскольку простые зависимости между двумя переменными в ней практически не встречаются.

Существует множество вариантов факторных планов, но на практике применяются далеко не все. Чаще всего используются факторные планы для двух независимых переменных и двух уровней типа 2 х 2. Для составления плана применяется принцип балансировки. План 2×2 используется для выявления эффекта воздействия двух независимых переменных на одну зависимую. Экспериментатор манипулирует возможными сочетаниями переменных и уровней. Данные приведены в простейшей таблице (табл. 5.6).

Таблица 5.6

2-я переменная	1-я переменная
	Есть	Нет
Есть
Нет

Реже используются четыре независимые рандомизированные группы. Для обработки результатов применяется дисперсионный анализ по Фишеру.

Так же редко используются другие версии факторного плана, а именно: 3×2 или 3×3. План 3×2 применяется в тех случаях, когда нужно установить вид зависимости одной зависимой переменной от одной независимой, а одна из независимых переменных представлена дихотомическим параметром. Пример такого плана — эксперимент по выявлению воздействия внешнего наблюдения на успех решения интеллектуальных задач. Первая независимая переменная варьируется просто: есть наблюдатель, нет наблюдателя. Вторая независимая переменная — уровни трудности задачи. В этом случае мы получаем план 3×2 (табл. 5.7).

Таблица 5.7

1-я переменная	2-я переменная
	Легкая	Средняя	Трудная
Есть наблюдатель
Нет наблюдателя

Вариант плана 3×3 применяется в том случае, если обе независимые переменные имеют несколько уровней и есть возможность выявить виды связи зависимой переменной от независимых. Этот план позволяет выявлять влияние подкрепления на успешность выполнения заданий разной трудности (табл. 5.8).

Таблица 5.8

Уровень сложности задачи	Интенсивность стимуляции
	Низкая	Средняя	Высокая
Низкий
Средний
Высокий

В общем случае план для двух независимых переменных выглядит как N х М. Применимость таких планов ограничивается только необходимостью набора большого числа рандомизированных групп. Объем экспериментальной работы чрезмерно возрастает с добавлением каждого уровня любой независимой переменной.

Планы, используемые для исследования влияния более двух независимых переменных, применяются редко. Для трех переменных они имеют общий вид L х М х N.

Чаще всего применяются планы 2 х 2 х 2: «три независимые переменные — два уровня». Очевидно, добавление каждой новой переменной увеличивает число групп. Общее их число 2, где п — число переменных в случае двух уровней интенсивности и К — в случае К-уровневой интенсивности (считаем, что число уровней одинаково для всех независимых переменных). Примером этого плана может быть развитие предыдущего. В случае, когда нас интересует успешность выполнения экспериментальной серии заданий, зависящая не только от общей стимуляции, которая производится в форме наказания — удара током, но и от соотношения поощрения и наказания, мы применяем план 3x3x3.

Упрощением полного плана с тремя независимыми переменными вида L х М х N является планирование по методу «латинского квадрата». «Латинский квадрат» применяют тогда, когда нужно исследовать одновременное влияние трех переменных, имеющих два уровня или более. Принцип «латинского квадрата» состоит в том, что два уровня разных переменных встречаются в экспериментальном плане только один раз. Тем самым процедура значительно упрощается, не говоря о том, что экспериментатор избавляется от необходимости работать с огромными выборками.

Предположим, что у нас есть три независимые переменные, с тремя уровнями каждая:

• 1) Lj, L2, L3;
• 2) Мг, М2, М3;
• 3) А, В, С.

План по методу «латинского квадрата» представлен в табл. 5.9.

Таблица 5.9

	*1	1*2	СО
М1		В2	С3
м2	В2	С3
м3	Сз		В2

Такой же прием используется для контроля внешних переменных (контрбалансировка). Нетрудно заметить, что уровни третьей переменной N {А, В, С) встречаются в каждой строке и в каждой колонке по одному разу. Комбинируя результаты по строкам, столбцам и уровням, можно выявить влияние каждой из независимых переменных на зависимую, а также степень попарного взаимодействия переменных.

«Латинский квадрат» позволяет значительно сократить число групп. В частности, план 2x2x2 превращается в простую таблицу (табл. 5.10).

2-я переменная	1-я переменная
	Есть	Нет
Есть	А	В
Нет	В	А

Применение латинских букв в клеточках для обозначения уровней третьей переменной (А — есть, В — нет) традиционно, поэтому метод назван «латинский квадрат».

Более сложный план по методу «греко-латинского квадрата» применяется очень редко. С его помощью можно исследовать влияние на зависимую переменную четырех независимых. Суть его в следующем: к каждой латинской группе плана с тремя переменными присоединяется греческая буква, обозначающая уровни четвертой переменной.

Рассмотрим пример. У нас четыре переменные, каждая из которых имеет три уровня интенсивности. План по методу «греко-латинского квадрата» примет такой вид (табл. 5.11).

Таблица 5.11

	*1
Мг	Ад	Яр	Су
М2	%
м3	су	Асх

Для обработки данных применяется метод дисперсионного анализа по Фишеру. Методы «латинского» и «греко-латинского» квадрата пришли в психологию из агробиологии, но большого распространения не получили. Исключением являются некоторые эксперименты в психофизике и психологии восприятия.

Главная проблема, которую удается решить в факторном эксперименте и невозможно решить, применяя несколько обычных экспериментов с одной независимой переменной, — определение взаимодействия двух переменных.

Рассмотрим возможные результаты простейшего факторного эксперимента 2 х 2 с позиций взаимодействий переменных. Для этого нам надо представить результаты опытов на графике, где по оси абсцисс отложены значения первой независимой переменной, а по оси ординат — значения зависимой переменной. Каждая из двух прямых, соединяющих значения зависимой переменной при разных значениях первой независимой переменной (А), характеризует один из уровней второй независимой переменной (В). Применим для простоты результаты не экспериментального, а корреляционного исследования. Условимся, что мы исследовали зависимость статуса ребенка в группе от состояния его здоровья и уровня интеллекта. Рассмотрим варианты возможных отношений между переменными.

Первый вариант: прямые параллельны — взаимодействия переменных нет (рис. 5.1).

Рис. 5.1

Больные дети имеют более низкий статус, чем здоровые, независимо от уровня интеллекта. Интеллектуалы имеют всегда более высокий статус (независимо от здоровья).

Второй вариант: физическое здоровье при наличии высокого уровня интеллекта увеличивает шанс получить более высокий статус в группе (рис. 5.2).

Рис. 5.2

В этом случае получен эффект расходящегося взаимодействия двух независимых переменных. Вторая переменная усиливает влияние первой на зависимую переменную.

Третий вариант: сходящееся взаимодействие — физическое здоровье уменьшает шанс интеллектуала приобрести более высокий статус в группе. Переменная «здоровье» уменьшает влияние переменной «интеллект» на зависимую переменную. Есть и другие случаи этого варианта взаимодействия: переменные взаимодействуют так, что увеличение значения первой приводит к уменьшению влияния второй с изменением знака зависимости (рис. 5.3).

Рис. 5.3

У больных детей, обладающих высоким уровнем интеллекта, меньше шанс полупить высокий статус, чем у больных детей с низким интеллектом, а у здоровых — связь интеллекта и статуса позитивная.

Теоретически возможно представить, что больные дети будут иметь больший шанс получить высокий статус при высоком уровне интеллекта, чем их здоровые низкоинтеллектуальные сверстники.

Последний, четвертый, возможный вариант наблюдаемых в исследованиях отношений между независимыми переменными: случай, когда между ними существует пересекающееся взаимодействие, представленное на последнем графике (рис. 5.4).

Рис. 5.4

Итак, возможны следующие взаимодействия переменных: нулевое; расходящееся (с различными знаками зависимости); пересекающееся.

Оценка величины взаимодействия проводится с помощью дисперсионного анализа, а t-критерий Стьюдента используется для оценки значимости различий групповых X.

Во всех рассмотренных вариантах планирования эксперимента применяется способ балансировки: различные группы испытуемых ставятся в разные экспериментальные условия. Процедура уравнивания состава групп позволяет производить сравнение результатов.

Однако во многих случаях требуется планировать эксперимент так, чтобы все его участники получили все варианты воздействия независимых переменных. Тогда на помощь приходит техника контрбалансировки.

Планы, в которых воплощается стратегия «все испытуемые — все воздействия», МакКолл называет ротационными экспериментами, а Кэмпбелл — «сбалансированными планами». Чтобы не было путаницы между понятиями «балансировка» и «контрбалансировка», будем использовать термин «ротационный план».

Ротационные планы строятся по методу «латинского квадрата», но, в отличие от рассмотренного выше примера, по строкам обозначены группы испытуемых, а не уровни переменной, по столбцам — уровни воздействия первой независимой переменной (или переменных), в клеточках таблицы — уровни воздействия второй независимой переменной.

Таблица 5.12

Группа	Уровни 1-й переменной
		х2	Х3
А	Ух	у2	У3
В	У2	У3	Ух
С	Уз	Ух	У2

Кэмпбелл включает этот план в число квазиэкспериментальных на основании того, что неизвестно, контролируется ли с его помощью внешняя валидность. Действительно, вряд ли в реальной жизни испытуемый может получить серию таких воздействий, как в эксперименте.

Что касается взаимодействия состава групп с другими внешними переменными, источниками артефактов, то рандомизация групп, согласно утверждению Кэмпбелла, должна минимизировать влияние этого фактора.

Суммы по столбцам в ротационном плане свидетельствуют о различиях в уровне эффекта при разных значениях одной независимой переменной (X или У), а суммы по строкам должны характеризовать различия между группами. Если группы рандомизированы удачно, то межгрупповых различий быть не должно. Если же состав группы является дополнительной переменной, возникает возможность ее проконтролировать. Схема контрбалансировки не позволяет избежать эффекта тренировки, хотя данные многочисленных экспериментов с применением «латинского квадрата» не позволяют делать такой вывод.

Подводя итог рассмотрению различных вариантов экспериментальных планов, предлагаем их классификацию. Экспериментальные планы различаются по таким основаниям.

• 1. Число независимых переменных: одна или больше. В зависимости от их числа применяется либо простой, либо факторный план.
• 2. Число уровней независимых переменных: при двух уровнях речь идет об установлении качественной связи, при трех и более — количественной связи.
• 3. Кто получает воздействие. Если применяется схема «каждой группе — своя комбинация», то речь идет о межгрупповом плане. Если же применяется схема «все группы — все воздействия», то речь идет о ротационном плане. Готтсданкер называет его кросс-индивидуальным сравнением.

Схема планирования эксперимента может быть гомогенной или гетерогенной (в зависимости от того, равно или не равно число независимых переменных числу уровней их изменения).

Стандартное отклонение — классический индикатор изменчивости из описательной статистики.

Стандартное отклонение, среднеквадратичное отклонение, СКО, выборочное стандартное отклонение (англ. standard deviation, STD, STDev) — очень распространенный показатель рассеяния в описательной статистике. Но, т.к. технический анализ сродни статистике, данный показатель можно (и нужно) использовать в техническом анализе для обнаружения степени рассеяния цены анализируемого инструмента во времени. Обозначается греческим символом Сигма «σ».

Спасибо Карлам Гауссу и Пирсону за то, что мы имеем возможность пользоваться стандартным отклонением.

Используя стандартное отклонение в техническом анализе, мы превращаем этот «показатель рассеяния» в «индикатор волатильности», сохраняя смысл, но меняя термины.

Что представляет собой стандартное отклонение

Индекс силы Индекс Силы — простой технический индикатор, который позволяет оценить силу текущего тренда. Не путайте Индекс Силы с Индексом относительной силы. …

Понимание сути стандартного отклонения возможно с пониманием азов описательной статистики. К примеру, мы имеем 2 выборки, у которых среднее арифметическое одинаково и равно 3. Казалось бы, одинаковое среднее делает эти две выборки одинаковыми. Ан-нет! Давайте рассмотрим возможные варианты данных для этих двух выборок:

1. 1, 2, 3, 4, 5
2. -235, -103, 3, 100, 250

Очевидно, что разброс (или рассеяние, или, в нашем случае, волатильность) гораздо больше во второй выборке. Следовательно, несмотря на то, что у этих двух выборок одинаковое среднее (равное 3), они совершенно разные в силу того, что у второй выборки данные беспорядочно и сильно рассеяны вокруг центра, а у первой — сконцентрированы около центра и упорядочены.

Но если нам надо быстро дать понять о таком явлении, мы не будем объяснять, как в абзаце выше, а просто скажем, что у второй выборки очень большое стандартное отклонение, а у первой — очень маленькое. Так, у второй выборки стандартное отклонение равно 186, а у первой оно равно 1,6. Разница существенная.

Стандартное отклонение в техническом анализе

Стандартное отклонение используется в техническом анализе не так часто, но оно служит отличным индикатором волатильности (изменчивости). Стандартное отклонение используется для промежуточных вычислений различных индикаторов, таких как, например, Полосы Боллинджера или Ширина Полос Боллинджера.

Но помимо промежуточных вспомогательных вычислений, стандартное отклонение вполне приемлемо для самостоятельного вычисления и применения в техническом анализе. Как отметил активный читатель нашего журнала burdock, «до сих пор не пойму, почему СКО не входит в набор стандартных индикаторов отечественных диллинговых центров».

Действительно, стандартное отклонение может классическим и «чистым» способом измерить изменчивость инструмента. Но к сожалению, этот индикатор не так распространен в анализе ценных бумаг.

Применение стандартного отклонения

Индекс среднего направления (ADX) Отличить период торгов от тенденции рынка и увидеть силу текущего тренда поможет индекс среднего направления ADX. Индекс среднего направления (англ. …

Для любого индикатора нам понадобится переменная, т.е. параметр. В данном случае нам нужен только период n, который указывает, какое количество периодов мы будем включать в вычисление стандартного отклонения.

Для вычисления, мы берем данные закрытия из n периодов назад от последней доступной цены. Т.е. если мы установили период индикатора 20 (достаточно часто используемый период),то мы берем 20 последних данных и оперируем ими для вычисления стандартного отклонения сегодня. Следовательно, для вычисления стандартного отклонения в любой момент времени k, надо взять цены закрытия всех n периодов назад от k.

Вычисление стандартного отклонения

Предупреждаю, что самостоятельное вычисление вам врядли понадобиться, т.к. основные программы обработки данных имеют встроенную функцию вычисления стандартного отклонения. Например, в Microsoft Excel эта функция называется СТАНДОТКЛОН.

Вручную вычислить стандартное отклонение не очень интересно, но полезно для опыта. Стандартное отклонение можно выразить формулой STD=√, что звучит как корень из суммы квадратов разниц между элементами выборки и средним, деленной на количество элементов в выборке.

Если количество элементов в выборке превышает 30, то знаменатель дроби под корнем принимает значение n-1. Иначе используется n.

Пошагово вычисление стандартного отклонения:

1. вычисляем среднее арифметическое выборки данных
2. отнимаем это среднее от каждого элемента выборки
3. все полученные разницы возводим в квадрат
4. суммируем все полученные квадраты
5. делим полученную сумму на количество элементов в выборке (или на n-1, если n>30)
6. вычисляем квадратный корень из полученного частного (именуемого дисперсией)

Средний истинный диапазон (ATR) Сложный и не очень востребованный технический индикатор «средний истинный диапазон» показывает уровень изменчивости анализируемого инструмента. Сре…

Для наглядности, вот пример из таблицы Excel:

Исходный файл Excel прилагается (.xls 24kb).

В данном примере я взял краткий отрезок исторических данных цен закрытия индекса ПФТС. Для вычислений, дата не нужна, но я решил ее оставить, чтоб вы могли сверить, если хотите. Что действительно важно, это все остальное. Обратите внимание на отдельные данные под темным разделителем: «среднее» и «всего». Есть столбец с ценой закрытия, столбец с разницами данных и среднего, и квадраты этих разниц.

После вычисления квадратов, мы складываем их, полученную сумму делим на количество элементов выборки (т.к. всего элементов 24, что меньше 30) и из полученного честного вычисляем квадратный корень. Результат округляем до целого, и получаем 69.

Важно заметить, что все эти вычисления дадут нам лишь значение индикатора «стандартное отклонение» в последний день, т.е. 26.09.2008, а для каждой другой даты надо проделывать этот комплекс операций отдельно.

Прикладное значение стандартного отклонения

Напомню, что смысл стандартного отклонения заключается в выявлении степени изменчивости инструмента. Т.е. стандартное отклонение не сможет показать аналитику ничего, кроме волатильности.

Важно отметить, что элементы выборки в среднем отличается от среднего значения на ±СО. Т.е. из примера выше, цены закрытия индекса ПФТС в среднем отличаются от среднего значения на ±69.

Из примера выше, отдельно цифра 69 ничего не скажет, т.к надо ее использовать с другими значениями стандартного отклонения в другие периоды. 69 — относительно немалая волатильность, но если в другие периоды стандартное отклонение будет больше 100, то, естественно, 69 окажется умеренной изменчивостью. Т.е. «все познается в сравнении».

Вывод

Стандартное отклонение — классический индикатор изменчивости из описательной статистики. Он поможет увидеть, как изменяется волатильность инструмента во времени.

← Понравилась статья? Лайкни и поделись с друзьями.

В разделе на вопрос Как рассчитать отклонение от плана В ПРОЦЕНТАХ! заданный автором Daria лучший ответ это Фактическую цифру умнож. на 100 и разделить на цифру плановую. От данного значения минус 100.Если результат отрицательный то значит на столько план не выполнен если положительный то соответственно перевыполнен план.
Источник: личный опыт

Ответ от Александр Соколов
UB1AFU Ученик (105) 1 месяц назад
возьми с полки пирожок 🙂
красавчег

Ответ от Надежда Надежда
Просто она перепутала очередность вначале умножить а потом минус.

Ответ от Валерия Заболоцкая
подскажие как подсчитать отклонения если по плану 0 а по факту 500 и по плану 10,5 а по факту 0

Многие экономисты ломают себе голову над тем, как рассчитать стандартное отклонение и что это такое. Кроме того, им еще нужно знать, что такое абсолютное отклонение и относительное. В этой статье описаны методы расчетов этих отклонений.

Стандартное отклонение

Стандартное отклонение, как рассчитать его? Для начала нужно понять, что же такое стандартное отклонение. Это очень существенный показатель рассеяния в разделе описательной статистики. Стандартное отклонение можно рассчитать по следующему алгоритму:

1. Сначала — вычисление среднего арифметического выборки данных.
2. Затем нужно вычесть среднее арифметическое от каждого элемента выборки.
3. Каждую полученную разницу следует возвести в квадрат.
4. Сложить все квадраты разниц, полученные в пункте 3.
5. Поделить сумму квадратов на количество элементов выборки.
6. Теперь из этого частного нужно извлечь квадратный корень.

Результат, который вы получите, и будет являться стандартным отклонением.

Абсолютное отклонение

Как рассчитать абсолютное отклонение? Абсолютным отклонением можно назвать разницу, получаемую при вычитании одной величины из другой, этот способ является выражением сложившихся положений вещей между плановым и фактическим параметрами.

Известно, что определенную проблему обычно вызывает такой показатель, как знак абсолютного отклонения. Обычно считается, что отклонение, которое позитивно сказывается на прибыли предприятия, считается положительным, и в вычислениях его ставят со знаком «+». Что же касается банальной математики, такой подход считается не совсем корректным, а это, в свою очередь, вызывает конфликты и разногласия среди специалистов. Исходя из этого, на практике вычисления абсолютного отклонения зачастую пользуются не базовой экономической, а математической моделью. Математическая модель заключается в том, что повышение фактического оборота в сравнении с запланированным обозначается знаком «+», а уменьшение фактических издержек в сравнении с плановыми обозначается знаком «-«.

Относительное отклонение

Как рассчитать относительное отклонение? Отклонение можно рассчитывать, опираясь на отношение к другим величинам, а это значит, что данный показатель выражается в процентах. Зачастую относительные отклонения вычисляются по отношению к относительно базовому значению или параметру. К примеру, можно выразить относительное отклонение, допустим, тех же затрат на материалы, как отношение к суммарной затрате или в проценте к обороту.

В применении относительных отклонений следует учесть, что их наличие способствует повышению уровня информативности анализа, который мы проводим, а следовательно, позволяет более отчетливо оценивать изменение, которое произошло в системе. Так, можно рассмотреть все на данном примере, возьмём величину абсолютного отклонения оборота, которая будет равна 1000 — 800 = 200. Данная цифра воспринимается в расчете относительного отклонения не так наглядно, как, к примеру, величина отклонения, показатели в которой выводятся в процентах: (1000 — 800) / 800 * 100% = 25%. Согласитесь, это все-таки режет глаз.

Селективное отклонение

Как рассчитать отклонение такого рода? Этот способ расчета отклонения подразумевает сравнение контролируемых величин на определенном промежутке времени, это может быть такой показатель времени, как квартал или месяц, иногда даже это бывает день. Сравнивание интересующих нас величин за определенный промежуток времени (к примеру, месяц, давайте возьмем май) текущего года с тем же маем предыдущего года может дать нам более информативное сравнение с предыдущим месяцем, который рассматривается в плановом периоде.

Селективное отклонение актуальны для фирм, которые занимаются поставкой сезонных услуг. Далее будут описаны еще несколько видов отклонений, знание которых может существенно облегчить вашу жизнь.

Кумулятивное отклонение

Кумулятивным отклонением можно назвать сумму, исчисляемую нарастающим итогом (кумулятивная сумма), и ее отклонение позволяет оценить уровень достижения за определенные периоды (месяцы) или же возможную разницу к окончанию определенного периода. Возникающее в отдельном периоде случайное колебание параметра деятельности предприятия может привести к значительному отклонению на коротком отрезке времени. Сама же кумуляция компенсирует случайные отклонения и позволяет более точным образом определить тренд.

Отклонение во временном разрезе

Как рассчитать отклонение во временном разрезе? Для данного отклонения типичным является сравнение типа факт — план. Отклонение определяется на основании сравнения бюджетного и фактического реализованного значения контролируемого параметра.

Этот подход к вычислению отклонений очень важен при негативном отклонении плановой величины от фактической. Также благодаря этому методу появляется возможность оперировать реальными фактами вместо того, чтобы опираться на плановые и желаемые показатели.

2. Абсолютное и относительное отклонение от плана.

Расчёт влияния факторов на изменение переменной части фонда оплаты труда проводят по формулам:

1) влияние объёма производства продукции:

2) влияние изменения структуры произведённой продукции:

3) влияние изменения удельной трудоёмкости продукции:

4) влияние изменения оплаты труда:

1.1.4 Факторная модель постоянной части ФЗП

Факторная модель постоянной части фонда оплаты труда представлена на рис.2.

Рис. 2. Детерминированная факторная система фонда заработной платы рабочих-повременщиков

Согласно этой схеме модель будет иметь следующий вид:

Фонд повременной заработной платы;

Среднесписочная численность работников;

Количество отработанных дней одним рабочим в среднем за год;

Средняя продолжительность смены.

Расчет влияния факторов по данной модели можно произвести способом абсолютных разниц:

Аналогично можно представить факторную модель для фонда заработной платы служащих.

В процессе анализа необходимо также установить эффективность использования фонда заработной платы.

1.1.5 Анализ соотношения производительности и оплаты труда

Для расширенного воспроизводства получения необходимой прибыли и рентабельности необходимо, чтобы темпы роста производительности труда опережали темп роста его оплаты. Если этот принцип не соблюдается, то происходит перерасход фонда зарплаты, повышение себестоимости продукции и, соответственно, уменьшение суммы прибыли.

Изменение среднего заработка работающих за период характеризуется его индексом:

Индекс изменения заработной платы;

Средняя заработная плата за отчетный период;

Средняя заработная плата за базисный период.

Изменение среднегодовой выработки определяется аналогично на основе индекса производительности труда:

, где

Средняя производительность труда за отчетный период;

Средняя производительность труда за базисный период.

Темп роста производительности труда должен опережать темп роста средней заработной платы. Для этого рассчитывают коэффициент опережения и анализируют его в динамике:

Коэффициент опережения роста производительности труда над ростом средней заработной платы;

Индекс изменения производительности труда;

Затем производят подсчёт суммы экономии (перерасхода) фонда заработной платы в связи с изменением соотношений между темпами роста производительности труда и его оплаты:

, где

Индекс изменения производительности труда;

Индекс изменения заработной платы.

1.2 Анализ показателей рентабельности предприятия 1.2.1 Рентабельность: понятие и виды

Рентабельность – это относительный показатель, определяющий уровень доходности бизнеса. Показатели рентабельности характеризуют эффективность как работы предприятия в целом, так и доходность различных направлений его деятельности. Они более полно, чем прибыль, характеризуют окончательные результаты хозяйствования, так как их величина показывает соотношение эффекта с наличными или использованными ресурсами.

Все существующие показатели рентабельности можно объединить в следующие группы, которые характеризуют

1) доходность капитала и его частей;

2) прибыльность продаж;

3) рентабельность (окупаемость) издержек производства и инвестиционных проектов.

Эти показатели могут рассчитываться на основе балансовой прибыли, прибыли от реализации продукции и чистой прибыли.

К первой группе относятся такие показатели, как общая рентабельность активов, чистая рентабельность оборотных активов, а также рентабельность собственного капитала. Одним из ключевых показателей эффективности деятельности предприятия является общая рентабельность активов. Она представляет собой отношение балансовой прибыли к стоимости имущества, т.е. хозяйственных средств (активам), находящимся в распоряжении предприятия и рассчитывается по следующей формуле:

Общая рентабельность активов;

Балансовая прибыль;

Средняя величина активов предприятия за анализируемый период (без учета убытков).

Чистая рентабельность оборотных активов показывает, какую чистую прибыль получает предприятие с каждого рубля, вложенного в активы:

Чистая рентабельность оборотных активов;

Чистая прибыль предприятия;

Среднее значение величины оборотных активов (второй раздел актива баланса).

Рентабельность активов сравнивается со средней процентной ставкой по заемным средствам, т.е. с альтернативной стоимостью. Если прибыль, получаемая на один рубль активов, меньше процентной ставки по заемным средствам, то можно сделать вывод о недостаточно эффективном управлении активами, так как денежные средства, вложенные в активы, принесли бы больший доход, будучи размещенными на депозитных счетах в банке.

Рентабельность собственного капитала показывает то, какую прибыль получает предприятие с каждого рубля собственных средств:

, где

Рентабельность собственного капитала;

Чистая прибыль предприятия;

Величина собственного капитала предприятия соответственно в начале и конце отчетного периода.

Ко второй группе можно отнести такой показатель, как рентабельность продаж, который рассчитывается делением прибыли от реализации продукции, работ и услуг до выплаты процентов и налогов на сумму полученной выручки:

Рентабельность оборота;

Прибыль от реализации продукции, работ и услуг до выплаты процентов и налогов;

Сумма выручки от реализации продукции, работ и услуг.

Данный показатель характеризует эффективность предпринимательской деятельности: сколько прибыли имеет предприятие с рубля продаж. Он рассчитывается в целом по предприятию и отдельным видам продукции.

И наконец, третья группа включает в себя рентабельность продукции (окупаемость издержек). Он исчисляется путем отношения прибыли от реализации до выплаты процентов и налогов к сумме затрат по реализованной продукции:

Рентабельность продукции;

Прибыль от реализации продукции до выплаты процентов и налогов;

Этот показатель показывает, сколько предприятие имеет прибыли с каждого рубля, затраченного на производство и реализацию продукции. Может рассчитываться как по отдельным видам продукции, так и в целом по предприятию. При определении его уровня в целом по предприятию целесообразно учитывать не только реализационные, но и внереализационные доходы и расходы, относящиеся к основной деятельности.

Аналогичным образом определяется и доходность инвестиционных проектов:

Рентабельность инвестиционных проектов;

Полученная или ожидаемая сумма прибыли от инвестиционной деятельности;

Сумма инвестиционных затрат.

1.2.2 Факторный анализ рентабельности продукции

В данном разделе будет подробно рассмотрен именно факторный анализ рентабельности продукции, так как подобный анализ других видов рентабельности производится аналогичным образом.

Итак, уровень рентабельности продукции (коэффициент окупаемости затрат), исчисленный в целом по предприятию, зависит от четырех основных факторов первого порядка: изменения объема реализации продукции , структуры реализованной продукции , ее себестоимости и средних цен реализации .

Расчет влияния факторов первого уровня на изменение рентабельности в целом по предприятию можно выполнить способом цепной подстановки:

1. по плану:

2. по плану, пересчитанному на фактический объем реализации продукции:

3. фактически при фактической структуре реализации продукции и плановой величине средней цены реализации и себестоимости реализованной продукции:

4. фактически при фактических структуре реализации продукции, величине средней цены реализации и плановой себестоимости реализованной продукции:

5. по факту:

Изменение рентабельности продукции общее:

В том числе за счет:

1. влияние объёма реализованной продукции:

2. влияние изменения структуры реализованной продукции:

3. влияние изменения среднего уровня цен реализации:

4. влияние изменения уровня себестоимости продукции:

После этого необходимо выполнить факторный анализ рентабельности по каждому виду продукции. Уровень рентабельности отдельных видов продукции зависит от изменения среднереализационных цен и себестоимости единицы продукции:

Расчет влияния выше перечисленных факторов на изменение рентабельности по определенному виду продукции также проводится способом цепной подстановки:

1. по плану:

2. по плану, пересчитанному на фактические среднереализационные цены:

3. по факту:

Общее изменение рентабельности продукции по определенному виду продукции:

В том числе за счет изменения:

1. среднего уровня отпускных цен

2. уровня себестоимости продукции:

Необходимо также более детально изучить причины изменения среднего уровня цен и способом пропорционального деления рассчитать их влияние на уровень рентабельности. Далее нужно установить, за счет каких факторов изменилась себестоимость единицы продукции, и аналогичным образом определить их влияние на уровень рентабельности.

Такие расчеты проводятся по каждому виду продукции (услуг), что позволяет точнее оценить работу хозяйствующего субъекта и полнее выявить внутрихозяйственные резервы роста рентабельности на анализируемом предприятии.

2 Практическая часть

Таблица 1

Для того чтобы проанализировать соотношение темпов роста производительности труда и средней заработной платы, необходимо определить:

1. плановую и фактическую величину производительности труда;

2. плановую и фактическую величину средней заработной платы;

3. темпы роста производительности труда и средней заработной платы.

Производительность труда;

Объем производства продукции;

Таким образом, из-за более быстрого темпа роста объема производства продукции по сравнению с темпом роста среднесписочной численности работников (см. табл.2) фактическая производительность труда увеличилась на 1,5 тыс. руб./чел. Среди других возможных факторов, повлиявших на уровень производительности труда можно выделить такие, как ликвидация потерь рабочего времени, увеличение норм выработки, повышение удельного веса покупных полуфабрикатов, повышение мощности оборудования, внедрение прогрессивных технологий, механизация и автоматизация производственных процессов.

Средняя заработная плата;

Среднесписочная численность работников.

Используя исходные данные получим:

Итак, фактическая средняя заработная плата составила 3042 тыс. рублей, что на 30 000 рублей больше плановой величины. Росту данного показателя способствовали такие факторы, как увеличение количества отработанных дней каждым рабочим, средней продолжительности рабочего дня, а также среднечасовой заработной платы.

, где

Плановая величина производительности труда;

Фактическая величина производительности труда.

, где

Темп роста средней заработной платы;

Плановая величина средней заработной платы;

Фактическая величина средней заработной платы.

Используя выше приведенную формулу получим:

Таким образом, приведенные расчеты свидетельствуют о том, что на анализируемом предприятии темпы роста производительности труда опережают темпы роста труда. Коэффициент опережения составляет 1,064.

Опережение темпов роста производительности труда над темпами роста средней заработной платы, несомненно, является положительным моментом в работе данного предприятия, так как несоблюдение этого принципа влечет за собой перерасход фонда заработной платы, повышение себестоимости и соответственно уменьшение суммы полученной прибыли.

В связи с изменением соотношений между темпами роста производительности труда и его оплаты можно определить сумму экономии (перерасхода) фонда заработной платы. Для этого необходимо использовать следующую формулу:

, где

Сумма экономии (-Э) или перерасхода (+Э) фонда заработной платы;

Фактическая величина фонда заработной платы;

Темп роста производительности труда;

Темп роста средней заработной платы.

Итак, более высокие темпы роста производительности труда по сравнению с темпами роста оплаты труда способствовали экономии фонда заработной платы в размере 37 378 руб.

Сведем все исходные и полученные данные в ниже приведенную таблицу (табл.2).

Таблица 2

2.2 Задача

Определить влияние факторов на рентабельность продукции способом цепных подстановок по следующим исходным данным:

Таблица 3

Из таблицы исходных данных видно, что и прибыль от реализации продукции и себестоимость реализованной продукции возросли по сравнению с плановыми показателями – на 69 800 рублей и 150 000 рублей соответственно. Рост величины прибыли от реализации продукции в целом по предприятию может быть обусловлен такими причинами, как увеличение объема реализации продукции, увеличение удельного веса более доходных видов продукции в общем объеме продаж, повышение уровня среднереализационных цен. Увеличение показателя себестоимости реализованной продукции может быть связан, во-первых, с увеличением выпуска продукции, во-вторых, с изменением структуры производства (например, увеличение удельного веса более трудоемкой продукции в общем объеме производства), в-третьих, с повышением уровня переменных затрат (повышение цен на используемое в производстве сырье, материалы, на электроэнергию, топливо и т.д.) и, наконец, из-за увеличения суммы постоянных расходов (повышение в отчетном периоде заработной платы административно-управленческому персоналу, увеличение его численности, увеличение общехозяйственных расходов).

Для дальнейшего анализа рентабельности важно рассчитать такой показатель, как темп роста прибыли и себестоимости:

Итак, согласно приведенным выше расчетам темп роста прибыли на предприятии выше темпа роста себестоимости.

1. Прежде чем определить влияние факторов на рентабельность продукции необходимо рассчитать плановую и фактическую величину данного показателя, который определяется по следующей формуле:

, где

Рентабельность продукции, или коэффициент окупаемости затрат;

Прибыль от реализации до выплаты налогов и процентов;

Сумма затрат по реализованной продукции.

Применительно к нашим данным получим:

Таким образом, с каждого рубля, затраченного на производство и реализацию продукции, анализируемое нами предприятие по плану должно было иметь прибыль в размере 42,91 копеек.

Таким образом, фактически с каждого, затраченного на производство и реализацию продукции, предприятие получило прибыль в размере 43,37 копеек.

По сравнению с планом рентабельность увеличилась на 0,46%, что является положительным моментом для предприятия. Увеличение данного показателя произошло за счет более быстрого темпа роста прибыли от реализации продукции по сравнению с темпами роста суммы затрат реализованной продукции.

Вообще положительное значение показателя рентабельности продукции свидетельствует об эффективности основной деятельности предприятия и о необходимости сохранения производства данного вида (видов) продукции.

2. Определим влияние факторов на рентабельность продукции способом цепных подстановок.

Уровень рентабельности продукции (коэффициент окупаемости затрат), исчисленный в целом по предприятию, зависит от двух факторов: изменения уровня прибыли от реализации продукции и изменения уровня себестоимости реализованной продукции.

Факторная модель этого показателя имеет следующий вид:

1. по плану:

2. по плану, пересчитанному на фактическую величину прибыли:

3. по факту:

Изменение рентабельности общее:

В том числе за счет:

Полученные результаты свидетельствуют о том, что за счет увеличения прибыли на 69 800 рублей уровень рентабельности продукции увеличился на 6,65%. Рост же суммы затрат по реализованной продукции на 150 000 рублей вызвал снижение уровня рентабельности продукции на 6,19%.

Заключение

Итак, можно утверждать, что анализ хозяйственной деятельности является базой для принятия управленческих решений в бизнесе. С помощью него изучаются тенденции развития, глубоко и системно исследуются факторы изменения результатов деятельности, устанавливаются причинно-следственные взаимосвязи и взаимозависимости по формированию экономических показателей и факторов, обосновываются бизнес-планы, выявляются резервы повышения эффективности производства, оцениваются результаты деятельности предприятия и их чувствительность к управленческим воздействиям, вырабатывается экономическая стратегия развития хозяйствующего субъекта.

В современных рыночных условиях овладение методикой экономического анализа менеджерами всех уровней является составной частью их профессиональной подготовки, так как, зная технику и технологию анализа, они смогут легко адаптировать предприятие к внешним изменениям и найти правильные ответы и решения.

Список использованной литературы

2. Грищенко О.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: учебное пособие. – Таганрог: изд-во ТРТУ, 2000.

3. Пивоваров К.В. Финансово-экономический анализ хозяйственной деятельности коммерче6ской организации. – М.: Дашко и Ко, 2003.

4. Пястолов С.М. Анализ финансово-хозяйственной деятельности предприятия: учебник. – М.: Академия, 2004.

5. Савицкая Г.В. .Анализ хозяйственной деятельности предприятия: учебник.– М.: Инфра-М, 2008.

Счетам Бухгалтерский баланс и другие отчетные формы Рис. 2. Схема журнально-ордерной формы учета АОЗТ «Колпнянское» 3. Организация учета оплаты труда на предприятии 3.1. Состояние учета оплаты труда на предприятии Для учета затрат труда, выполненных работ и начисления заработной платы на АОЗТ «Колпнянское» используется несколько форм первичных…

О финансовых результатах»), данные оперативного учета. Анализ прибыли и рентабельности осуществляется в определенной последовательности. Основные этапы анализа приведены на рис. 8.7. Первый этап – анализ формирования прибыли и рентабельности на предприятиях торговли и общественного питания. Он включает три стадии. На первой стадии рассматривается динамика суммы и уровня показателей прибыли и…

Тех производственных фондов, с которых взимается плата за фонды. Применяется также показатель уровня рентабельности к текущим затратам – отношение прибыли к себестоимости товарной или реализованной продукции. Каждое предприятие самостоятельно осуществляет свою производственную и хозяйственную деятельность на принципах самоокупаемости и прибыльности. Предприятие имеет определенные расходы по…

Таблица 1.1

Выполнение плана в % =72166 / 68952 *100 % = 104,66 %

Т.о. можно сделать вывод, что план перевыполнен на 4,66 %

Абсолютное отклонение = Отчетный год факт – Отчетный год план

Абсолютное отклонение = 72166 – 68952 = 3214 млн. руб.

Т.о. можно сделать вывод о том, что план по производству товарной продукции перевыполнен на 3214 млн. руб.

Относительное отклонение = Выполнение плана % — 100

Относительное отклонение = 104,66 – 100 = 4,66 %

Полученное отклонение говорит о том, что план перевыполнен на 4,66 % .

Абсолютный прирост за год = Отчетный год факт – предшествующий год

Абсолютный прирост за год = 72166 –67485 = 4681 млн. руб.

Т.о. по сравнению с предыдущим годом произошло увеличение объема выпуска продукции на 4681 млн. руб.

Темп роста % = Отчетный год фактически / предшествующий год * 100 %

Темп роста % = 72166 / 67485 * 100 % = 106,94%

В отчетном году по сравнению с предыдущим годом производство продукции в % соотношении составило 106,9 %. Чтобы определить на сколько % увеличился объем выпуска товарной продукции в отчетном году по сравнению с предыдущим годом рассчитаем:

Темп прироста % = Темп роста % — 100 %

Темп роста % = 106,94% – 100 % = 6,94%

В предыдущим годом объем выпуска продукции увеличился до 72166 млн.руб., причем произошло перевыполнение плана на 4,66 %, что в абсолютном выражении составляет 3214 млн. руб. Плановое увеличение объема продукции составило 1467 млн. руб (1), а фактически было произведено продукции на сумму 5442 млн. руб., таким образом темп прироста по плану составил 2,2% (2), а фактически составил 6,94%

1: 68952-67485=1467

2: (68952-67485)/67485*100%=2,2%

Причиной перевыполнения плана может служить изменение конъюнктуры рынка, повышение спроса на отдельные виды продукции, улучшение организационной структуры предприятия.

2. АНАЛИЗ ВЫПОЛНЕНИЯ ПЛАНА ПО АССОРТИМЕНТУ

Определим процент выполнения плана по ассортименту, а полученные расчеты сведем в аналитическую таблицу 2.1.

Таблица 2.1

Определение процента выполнения плана по ассортименту .

Выполнение плана в % = Выпуск изделий факт / Выпуск изделий план *100 %

Выполнение плана в %:

50400 / 45360 *100 % = 111,11 % (план перевыполнен на 11,11 %)

41600 / 46800 *100 % = 88,89 % (план недовыполнен на 11,11 %)

16500 / 14400 *100 % = 114,58 % (план перевыполнен на 14,58 %)

Коэффициент выполнения плана по муз. центрам составил 111,11%, по пылесосам 88,89 % ,а телевизорам 114,58%.

Условный выпуск (принимается в расчет выполнение плана по ассортименту).

Если факт ниже плана – выбираем факт.

Если факт выше плана – выбираем план.

Условный выпуск / Выпуск изделий в стоимостном выражении по плану *100 %

Коэффициент выполнения плана по ассортименту = 101360/ 106560 *100 % =

По пылесосам произошло недовыполнение плана на 11,11%, но несмотря на это, муз. центров произведено на 11,11% больше запланированного, а телевизоров перевыполнено на 14,58%. В целом же наблюдается недовыполнение плана по ассортименту на 4,9%.

Проведем графическое моделирование: построим столбиковые диаграммы в ассортиментном составе.

Относительные показатели представляют собой отношение одной абсолютной величины к другой. Они отражают количественные соотношения между исследуемыми явлениями. При вычислении относительного отклонения производится сравнение одного или нескольких показателей с базой или основанием.

Вам понадобится

• — калькулятор.

Инструкция

• Специфической чертой показателя отклонения является то, что он позволяет отвлечься от определенных различий абсолютных величин. Это дает возможность сравнивать такие явления, абсолютные значения которых являются не сопоставимыми.
• Относительное отклонение представляет собой отклонение, рассчитываемое по отношению к другим величинам. Выражается в процентах или долях. Чаще всего исчисляется по отношению к какому-либо общему показателю или параметру. Применение этого индекса в исследованиях повышает уровень информативности проводимого анализа и позволяет более точно оценивать изменения.
• Общая формула расчета может быть представлена следующим образом: ∆о = хотч/хб. Ее составляющие изменяются в зависимости от того, какое явление берется в основу сопоставления.
• Если необходимо соотнести один и тот же показатель в разные периоды времени, рассчитываем темп его роста. Он показывает, как изменилась величина в отчетном (текущем) периоде по сравнению с ее базисным уровнем: Тр = х1/х0. Если этот показатель выражается в процентах, то речь идет о темпе прироста: Тпр = (х1/х0)*100%.
• Относительная величина планового задания представляет собой отношение планируемого и принятого за основу для сравнения уровней одного и того же явления. В качестве базы выступает фактически достигнутая величина признака исследуемого явления в предшествующем периоде. Формула расчета имеет вид: ОВпз = хпл/хб.
• Если рассматривается выполнение заданного уровня, то речь идет о понятии «выполнение плана». В этом случае рассчитывается относительно отклонение фактически полученного результата от планируемого уровня: ОВвп = хф/хпл. Оно показывает, во сколько раз полученное значение исследуемого явления отличается от запланированного уровня явления на этот же период.

Абсолютное отклонение – это разность между фактической и базовой величиной показателя. Абсолютные отклонения могут быть рассчитаны для любых количественных и качественных показателей (объема продукции, количественных и качественных показателей, характеризующих использование ресурсов, величины активов, прибыли, финансовых коэффициентов и т. п.). Например,

ΔN = N1 – N0; ΔR = R1 – R0; ΔD = D1 – D0,

где		–	объем продукции;
		–	среднесписочная численность работающих;
			выработка продукции на одного работающего.

Базовые значения показателей в анализе принято обозначать индексом 0, фактические – 1, отклонения (изменения) – символом Δ.

Относительное отклонение позволяет измерить прирост ресурса с учетом темпов роста продукции, выпущенной с использованием данного ресурса. Относительные отклонения вычисляются только для количественных показателей, характеризующих величину потребленных ресурсов (затрат ресурсов).

Чтобы найти относительное отклонение, нужно из фактической величины ресурса вычесть его базовую величину, скорректированную на коэффициент изменения объема продукции.

ΔR’ = R1 – R0 × kN; kN = N1 / N0.

Величина R0 × kN показывает, сколько ресурсов было бы необходимо для производства фактического объема продукции, если бы не изменялись качественные характеристики использования ресурсов.

Отрицательное относительное отклонение называется относительной экономией ресурса, положительное – относительным перерасходом.

Если представить фактическую величину ресурса через его базовую величину и темп роста, формулу исчисления относительного отклонения можно преобразовать следующим образом:

ΔR’ = R1 – R0 × kN = R0 × kR – R0 × kN = R0 × (kR – kN).

Такое представление демонстрирует, что относительное отклонение возникает за счет разницы темпов роста ресурса и продукции. Если темп роста продукции опережает темп роста ресурса, возникает относительная экономия, что свидетельствует о достаточно эффективном использовании ресурса. Если же темп роста ресурса превышает темп роста продукции, ресурс используется неэффективно, о чем свидетельствует относительный перерасход.

Если же темпы роста ресурса и продукции совпадают, относительное отклонение равно нулю. Это означает, что прирост продукции получен экстенсивным путем, т. е. только за счет привлечения дополнительных ресурсов. При этом качественные показатели использования ресурса не изменяются.

На основании данных таблицы 3.1 оценим эффективность использования трудовых ресурсов.

Таблица 3.1

Исходные данные для оценки эффективности использования трудовых ресурсов

Относительное отклонение может быть вычислено только для показателя, характеризующего численность работающих.

ΔR’ = R1 – R0 ×∙kN = 96 – 90 ×∙1,111 = 96 – 100 = -4.

Данные таблицы 3.1, а также расчет относительного отклонения позволяют сделать вывод, что трудовые ресурсы использовались достаточно эффективно. Об этом свидетельствует опережающий темп роста объема продукции по сравнению с темпом роста численности работающих, что и привело к относительной экономии данного вида ресурса, а также к росту выработки продукции на одного работающего.